はじめに
オペレーションズリサーチ(OR)は、複雑な現実の問題を数学的モデルに落とし込み、最適な解決策を見つけるための科学的手法です。
ここでは、ORの基本的な手法と、実際に手を動かすためのツールについて、初心者でも取り組みやすい形で解説します。
OR、物流、生産計画、在庫管理、サービス業のスケジューリングなど、さまざまな分野で応用可能です。
ORの基本的な手法
ORでは多くの手法が利用されますが、ここでは特に代表的なものをいくつかご紹介します。
1. 線形計画法
- 概要:
複数の制約条件のもと、目的関数(例:利益の最大化やコストの最小化)を最適化する手法です。 - 用途:
製造現場の生産計画や物流、在庫管理などでよく使われます。 - ポイント:
制約条件は一次不等式で表現され、問題が大きくなっても比較的扱いやすいのが特徴です。
2. 整数計画法
- 概要:
変数が整数になるという条件を追加した線形計画法。 - 用途:
配送ルートの最適化やスケジューリング、施設配置問題など、現実の数値が整数であるケースに適用されます。 - ポイント:
問題が非線形に発展するため、解くためのアルゴリズムやツールが重要になります。
3. シミュレーション
- 概要:
実際のシステムやプロセスの動きをコンピュータ上で再現し、様々なシナリオを検証する手法。 - 用途:
待ち行列理論や在庫管理、サービスシステムなど、変動や不確実性が大きい状況の分析に有効です。 - ポイント:
乱数を用いたモデリングにより、現実の状況をより正確に再現できます。
4. 意思決定支援手法
- 例:AHP(階層的意思決定法)
複数の判断基準をもとに意思決定を行うための方法。 - 例:ゲーム理論
競争環境下での戦略的意思決定を分析するために用いられます。 - 用途:
複数の評価基準や競合状況を考慮する場合に役立ち、戦略立案やリスク評価などに応用されます。
ORのツール紹介
実際にORの手法を使って問題を解くためには、適切なツールを選ぶことが重要です。ここでは、初心者でも取り組みやすいツールをいくつかご紹介します。
1. Excel Solver
- 概要:
Excelに標準搭載されている最適化ツールで、線形計画法や非線形計画法の問題を簡単に解くことができます。 - メリット:
手軽に始められるため、ORの基礎を学ぶ入門ツールとして非常に人気です。 - デメリット:
Excelがなければ利用ができず、他のツールと比べて感覚的に把握するのは困難です。 - 活用例:
簡単な在庫管理や生産計画問題など、初歩的な最適化問題に最適です。
Excel で Solver アドインを読み込む - Microsoft サポート
ソルバー アドインを Excel に読み込む方法 (モバイル デバイスでは使用できません)。
2. Pythonライブラリ
- PuLPやSciPy:
Pythonでは、オープンソースの最適化ライブラリ(PuLP、SciPy)を使って線形計画法や整数計画法を実装できます。 - Google OR-Tools:
Googleが提供するツールキットで、線形計画法、整数計画法、スケジューリング、組み合わせ最適化など多岐にわたる問題に対応しています。 - メリット:
プログラムの自由度が高く、実際のデータに基づいたカスタマイズが可能です。
# 必要なライブラリをインポート
import pulp # 線形計画問題を解くためのライブラリ
import matplotlib.pyplot as plt # グラフ描画用のライブラリ
import japanize_matplotlib
import numpy as np # 数値計算用ライブラリ
# -------------------------------
# 1. 線形計画問題の定義
# -------------------------------
# 問題を作成します。ここでは「工場の最適生産計画」という名前で、利益の最大化(最大化問題)を解く設定です。
prob = pulp.LpProblem("工場の最適生産計画", pulp.LpMaximize)
# -------------------------------
# 2. 変数の定義
# -------------------------------
# 製品Aと製品Bの生産量を決定する変数を定義します(0以上の連続変数)
x = pulp.LpVariable("製品Aの生産量", lowBound=0, cat='Continuous')
y = pulp.LpVariable("製品Bの生産量", lowBound=0, cat='Continuous')
# -------------------------------
# 3. 目的関数(利益の最大化)の設定
# -------------------------------
# 目的関数は「総利益 = 40 * 製品Aの生産量 + 30 * 製品Bの生産量」
# この利益を最大化するのが目的です。
prob += 40 * x + 30 * y, "総利益の最大化"
# -------------------------------
# 4. 制約条件の設定
# -------------------------------
# 制約条件は現実の資源制限などを表します。
# (1) 材料の制約: 2 * 製品A + 製品B ≤ 100
prob += 2 * x + y <= 100, "材料制約"
# (2) 労働時間の制約: 製品A + 製品B ≤ 80
prob += x + y <= 80, "労働制約"
# (3) 製品Aの生産上限: 製品A ≤ 40
prob += x <= 40, "製品A上限"
# (4) 製品Bの生産上限: 製品B ≤ 50
prob += y <= 50, "製品B上限"
# -------------------------------
# 5. 問題を解く(最適化の実行)
# -------------------------------
prob.solve() # PuLPが自動的に最適解を求めます
# -------------------------------
# 6. 最適解の出力
# -------------------------------
print("最適な生産計画:")
print(f"製品Aの生産量: {pulp.value(x)}")
print(f"製品Bの生産量: {pulp.value(y)}")
print(f"最大総利益: {pulp.value(prob.objective)}")
# -------------------------------
# 7. 結果の可視化(グラフ描画)
# -------------------------------
# 製品Aの生産量に対応する値を生成(グラフ用の横軸の値)
x_vals = np.linspace(0, 50, 100)
# グラフの作成
fig, ax = plt.subplots()
# 材料制約のグラフ: 2*x + y = 100 から y = 100 - 2*x
ax.plot(x_vals, 100 - 2 * x_vals, label='材料制約 (2*製品A + 製品B <= 100)')
# 労働制約のグラフ: x + y = 80 から y = 80 - x
ax.plot(x_vals, 80 - x_vals, label='労働制約 (製品A + 製品B <= 80)')
# 製品Aと製品Bの生産上限を破線で表示
ax.axvline(40, color='red', linestyle='--', label='製品A上限 (<= 40)')
ax.axhline(50, color='blue', linestyle='--', label='製品B上限 (<= 50)')
# 求めた最適解をプロット(黒い点)
ax.scatter(pulp.value(x), pulp.value(y), color='black', marker='o', label='最適解')
# 軸ラベルとタイトルの設定
ax.set_xlabel('製品Aの生産量')
ax.set_ylabel('製品Bの生産量')
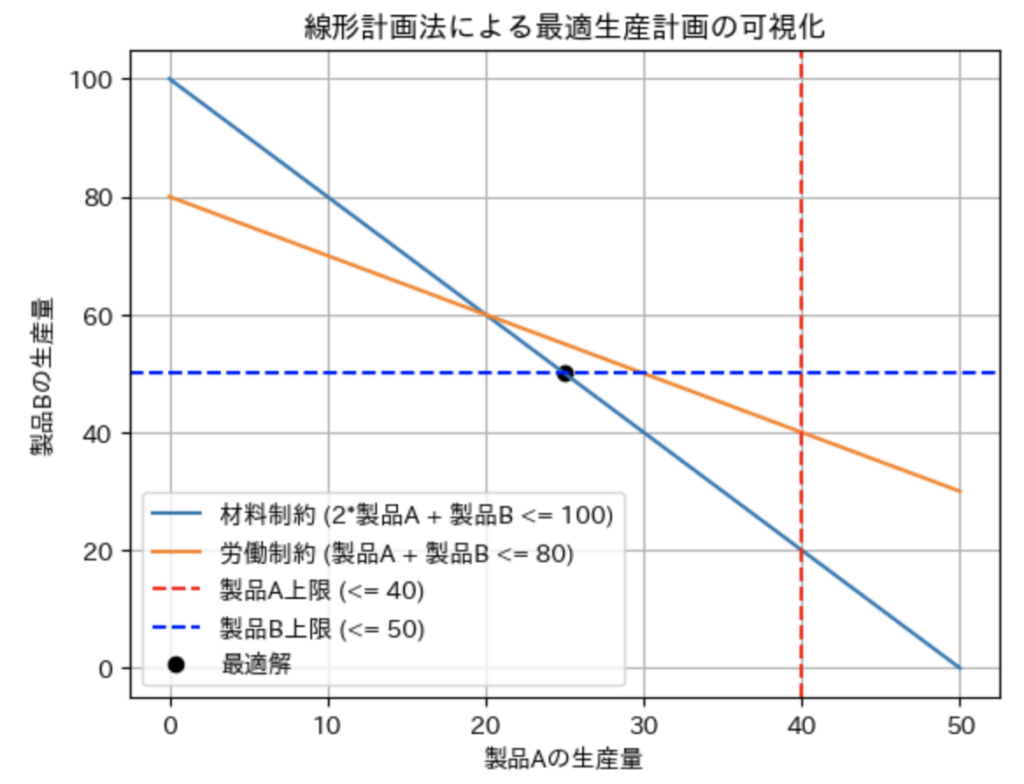
ax.set_title('線形計画法による最適生産計画の可視化')
# 凡例とグリッドの設定
ax.legend()
ax.grid(True)
# グラフの表示
plt.show()
3. 商用ソフトウェア
- GurobiやCPLEX:
大規模な最適化問題を解くための強力なソルバーで、産業界でも広く利用されています。 - メリット:
非常に高速で精度の高い解法を提供するため、実務レベルの問題にも対応可能です。 - 注意点:
ライセンス費用がかかる場合が多いため、学習や研究段階では無料版や学生向けライセンスの利用が推奨されます。
4. その他のツール
- 専用ソフトウェア:
例えば、シミュレーション専用のソフトウェアや、待ち行列システムを解析するツールなども存在します。 - オンラインツール:
ウェブ上で簡単な最適化問題を解くためのオンラインサービスもあるので、手軽に試すことができます。 - 参考情報:
詳細なソフトウェア一覧やリンク集は、ORのポータルサイトなどで確認できます。fit.ac.jp
まとめ
ORの基本手法とツールは、問題解決のための強力な武器となります。
まずはExcel Solverなどで基礎を固め、次第にPythonライブラリや商用ソルバーを活用することで、より実践的な問題解決にチャレンジできるでしょう。
これらの手法やツールは、業界を問わず多様な応用が可能ですので、ぜひ日常の課題解決に役立ててみてください!


