はじめに
皆さんは「教師なし学習」という言葉を耳にしたことがありますか?機械学習の世界では重要な概念ですが、初めて聞く方には少し難しく感じるかもしれません。この記事では、教師なし学習の基本から応用まで、初心者にも理解しやすいように解説していきます。具体的な例を交えながら、なぜこの技術が現代のデータ分析に欠かせないのかも説明していきましょう。
教師なし学習とは
教師なし学習(Unsupervised Learning)は、機械学習の主要な学習方法の一つです。「教師なし」という言葉が示すように、データに対する「正解」や「ラベル」を与えずに学習を進めていきます。
具体的には、コンピュータにデータを与えて「このデータの中にどんなパターンがありますか?」と尋ねるようなものです。例えば、スーパーマーケットでの1000人の顧客の購買履歴を分析すると、「週末に訪れる家族連れ」「平日夕方に立ち寄る会社員」「オーガニック商品を好む健康志向の方」といったグループが自然と見えてくることがあります。教師なし学習はこうしたパターンを自動的に発見してくれるのです。
教師なし学習の主な目的は以下の3つです:
- データの隠れたパターンや構造を発見する – 人間が気づかなかった関連性を見つける
- データを特徴に基づいてグループ化する – 似た特性を持つデータをまとめる
- データの複雑さを減らし、重要な特徴を抽出する – 本質的な情報だけを取り出す
この学習方法は、私たちが事前に知らなかった新たな洞察を得るのに役立ちます。例えば、「このタイプの顧客はこのような商品を好む傾向がある」といった、事前に気づいていなかった関係性を発見できるのです。
教師あり学習との違い
教師なし学習をよりよく理解するために、教師あり学習と比較してみましょう。初心者の方には、この違いを理解することが重要です。
| 特徴 | 教師あり学習 | 教師なし学習 |
|---|---|---|
| 学習データ | ラベル(正解)付きデータ | ラベルなしデータ |
| 目的 | 予測や分類(結果を当てる) | パターン発見や構造理解 |
| 例 | メールがスパムかどうかを判定する | 顧客を購買パターンでグループ化する |
| 評価方法 | 予測精度など客観的な指標 | クラスタの品質など主観的な評価が多い |
教師あり学習は「答え合わせ」ができる問題に向いており、例えば「このメールはスパムですか?」「この取引は不正ですか?」といった質問に「はい/いいえ」で答えられるタスクに適しています。
一方、教師なし学習は「新たな発見」を目指す問題に適しており、「このデータの中にどんなグループがありますか?」「最も重要な特徴は何ですか?」といった質問に答えるのに役立ちます。
例えるなら、教師あり学習は「地図を持って目的地にたどり着く」ことに、教師なし学習は「地図なしで探検して新しい場所を発見する」ことに似ています。
主な手法と活用例
教師なし学習にはいくつかの重要な手法があります。それぞれの特徴と実際の活用例を見ていきましょう。
クラスタリング
クラスタリングは、データを似た特徴を持つグループ(クラスタ)に分ける手法です。これにより、データの自然な構造を理解することができます。
K-means(k平均法)クラスタリング
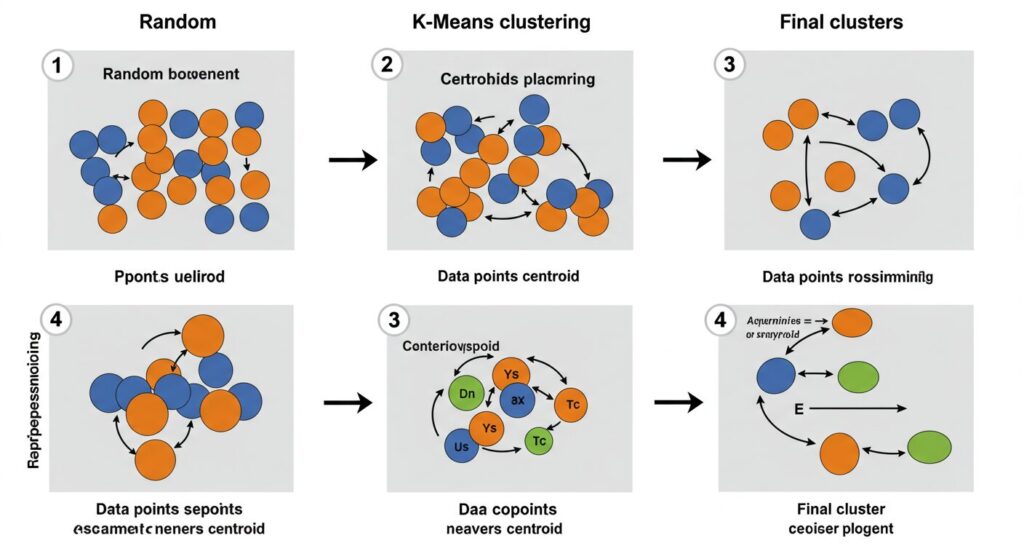
最も広く使われているクラスタリングアルゴリズムの一つが「K-means」です。このアルゴリズムは以下のようなシンプルなステップで動作します:
- クラスタの数(K)を決める(例:顧客を3グループに分けたい)
- ランダムにK個の中心点(セントロイド)を配置する
- 各データポイントを最も近い中心点に割り当てる
- 各クラスタの中心点を、そのクラスタに含まれるデータの平均位置に更新する
- 収束するまで3と4を繰り返す
活用例
- 顧客セグメンテーション:似た購買行動を持つ顧客をグループ化し、ターゲットマーケティングに活用
- 画像の色圧縮:画像の色数を減らす処理に使用
- 文書のトピック分類:類似した内容の文書をグループ化
次元削減
次元削減は、データの持つ多くの特徴(次元)から重要な特徴だけを抽出し、データをより単純な形で表現する手法です。多くの場合、私たちが扱うデータは多くの特徴(変数)を持っていますが、実はそのうちの一部だけが本当に重要であることが多いのです。
例えば、顧客データに年齢、性別、収入、職業、居住地域、家族構成など20項目あったとしても、実際の購買行動に影響する主要な特徴は3〜4項目かもしれません。次元削減はこうした本質的な特徴を見つけ出す手法です。
主成分分析(PCA:Principal Component Analysis)
次元削減の代表的な手法である主成分分析は、データの分散(バラつき)が最大になる方向を見つけ、それを新しい軸として使うことでデータを効率的に表現します。
主成分分析の基本的な流れは以下の通りです:
- データを標準化する(平均0、分散1にする)
- データの共分散行列を計算する
- 共分散行列の固有値と固有ベクトルを求める
- 固有値が大きい順に固有ベクトルを選び、それを新しい軸とする
- もとのデータを新しい軸に射影する
難しく聞こえるかもしれませんが、イメージとしては「データが最も広がる方向」と「次に広がる方向」を新しい座標軸として使う、と考えるとわかりやすいでしょう。
活用例
- 顔認識:多次元の顔画像データから特徴量を抽出
- データの可視化:高次元データを2次元や3次元に削減して可視化
- ノイズ除去:データから主要な成分だけを抽出し、ノイズを削減
異常検知
異常検知は、通常のパターンから逸脱したデータ(異常値)を発見する技術です。特に教師なし学習による異常検知は、「正常」な例だけを使って学習し、それと大きく異なるものを「異常」として検出します。
Isolation Forest(アイソレーションフォレスト)
Isolation Forestは、異常値は他のデータから「孤立」しやすいという性質を利用したアルゴリズムです。このアルゴリズムは、ランダムに選んだ特徴とその分割点でデータを繰り返し分割し、データポイントを分離するのに必要な分割回数が少ないものを異常と判定します。
通常のデータポイントは多くの分割が必要ですが、異常値は少ない分割で「孤立」させることができる、という直感的な考え方に基づいています。
活用例
- 不正検出:クレジットカードの不正利用検出
- 製造業の品質管理:製品の異常を自動検出
- ネットワークセキュリティ:通常と異なるネットワークトラフィックパターンを検出
Pythonでの実装例
ここからは、実際にPythonを使って教師なし学習を実装する方法を見ていきましょう。scikit-learn(sklearn)というライブラリを使うと、簡単に様々なアルゴリズムを試すことができます。
K-meansクラスタリングの実装例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# サンプルデータの生成
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# K-meansモデルの作成と学習
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
# クラスタの割り当て
y_kmeans = kmeans.predict(X)
# 結果の可視化
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
# クラスタの中心を表示
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
plt.title('K-meansクラスタリング結果')
plt.show()
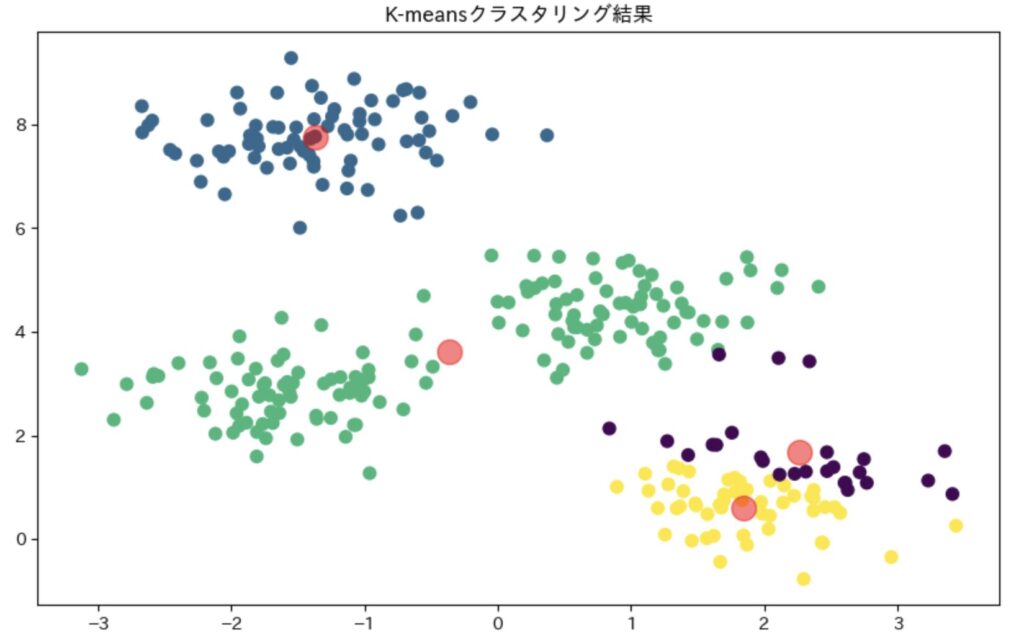
このコードでは、まず300個のデータポイントを作成し、4つのクラスタに分類しています。その後、各データポイントがどのクラスタに属するかを色分けして可視化し、クラスタの中心を赤い点で表示しています。
主成分分析(PCA)の実装例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
# 手書き数字データセットの読み込み
digits = load_digits()
X = digits.data
y = digits.target
# 2次元に次元削減
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 結果の可視化
plt.figure(figsize=(12, 8))
for i in range(10):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], label=str(i))
plt.legend()
plt.title('手書き数字の2次元PCA表現')
plt.show()
# 寄与率(各主成分がどれだけデータの分散を説明できているか)
print(f"第1主成分の寄与率: {pca.explained_variance_ratio_[0]:.4f}")
print(f"第2主成分の寄与率: {pca.explained_variance_ratio_[1]:.4f}")
print(f"合計寄与率: {sum(pca.explained_variance_ratio_[:2]):.4f}")
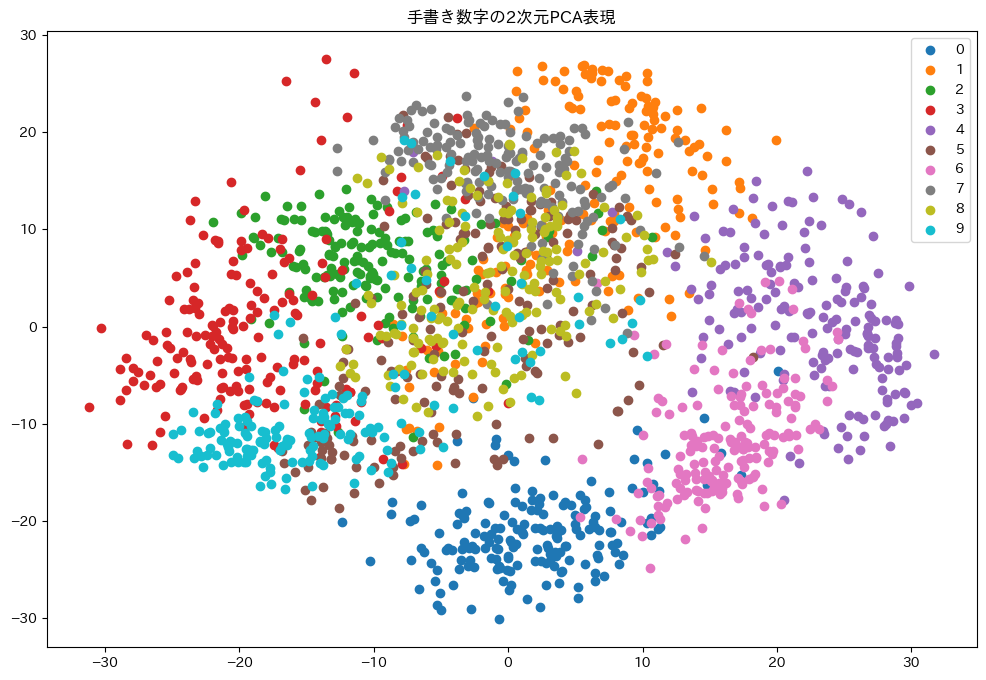
このコードでは、手書き数字のデータセット(各数字は64次元のデータ)を2次元に圧縮し、可視化しています。各色が0から9までの数字を表しており、似た数字は2次元平面上でも近くに配置されていることがわかります。
異常検知の実装例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
from sklearn.datasets import make_blobs
# 正常データの生成
X, _ = make_blobs(n_samples=200, centers=1, cluster_std=1, random_state=42)
# 異常データの追加
outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.vstack([X, outliers])
# Isolation Forestモデルの作成と学習
clf = IsolationForest(contamination=0.1, random_state=42)
y_pred = clf.fit_predict(X)
# 異常値は-1、正常値は1として返されるので、可視化用に変換
colors = np.where(y_pred == 1, 'blue', 'red')
# 結果の可視化
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=colors)
plt.title('Isolation Forestによる異常検知')
plt.legend(['正常', '異常'])
plt.show()
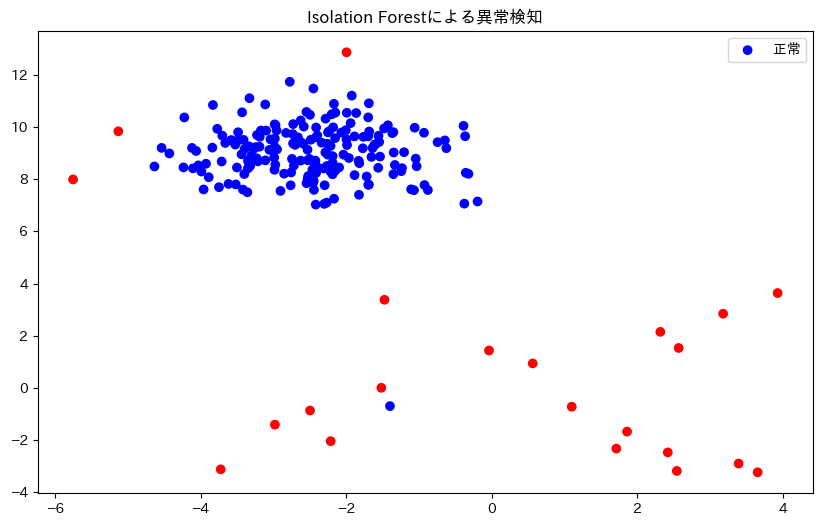
このコードでは、まず200個の「正常」データポイントを生成し、そこに20個の「異常」データポイントを追加しています。Isolation Forestアルゴリズムを使って異常検知を行い、結果を青(正常)と赤(異常)で色分けして表示しています。
まとめと今後の展望
この記事では、教師なし学習の基本概念から主要な手法、そして実際の実装例まで解説してきました。教師なし学習は、ラベル付きデータがない場合や、データ内の未知のパターンを発見したい場合に特に威力を発揮します。
教師なし学習の主な特徴をまとめると:
- ラベルなしデータから学習を行う
- データの隠れたパターンや構造を発見する
- クラスタリング、次元削減、異常検知などの手法がある
- 新たな洞察や知識の発見に役立つ
今後の展望として、教師なし学習は以下のような方向に発展していくと考えられます:
- ディープラーニングとの融合:オートエンコーダなどのディープラーニング技術を用いた高度な特徴抽出
- 半教師あり学習への応用:少量のラベル付きデータと大量のラベルなしデータを組み合わせた学習手法
- 自己教師あり学習の発展:データ自体から教師信号を作り出す新しい学習パラダイム
教師なし学習は、人間が気づかないデータの関係性やパターンを発見するという点で、まさに「機械の知能」を活かした技術といえるでしょう。データ分析や機械学習の基礎を学ぶ皆さんにとって、教師なし学習の理解は大きな武器になるはずです。
最後に、この記事がみなさんの学習の一助となれば幸いです。教師なし学習の世界を探索して、データから新たな価値を生み出していきましょう。