はじめに
統計学において「有意差」という言葉は、データ分析や仮説検定を行う際に頻繁に登場します。有意差は、観測されたデータの差が偶然によるものではなく、統計的に意味のある差であることを示します。本記事では、有意差の基本的な概念から、具体的な検定方法、そしてビジネスや研究での活用例までをわかりやすく解説します。
有意差とは?
有意差とは、統計的検定を通じて「観測された差が偶然ではなく、実際に意味のある差である」と判断される場合に用いられる言葉です。たとえば、ある新薬の効果を検証する際に、治療群とプラセボ群の間で得られた結果に有意差がある場合、その新薬が実際に効果を持つ可能性が高いと考えられます。
帰無仮説と対立仮説の関係
有意差を検討する際には、以下の2つの仮説を設定します:
- 帰無仮説(H₀):「差がない」「効果がない」という仮説。検定の出発点となる仮説です。
- 対立仮説(H₁):「差がある」「効果がある」という仮説。帰無仮説が棄却された場合に採択されます。
たとえば、新薬の効果を検証する場合:
- 帰無仮説:新薬とプラセボの効果に差はない。
- 対立仮説:新薬とプラセボの効果に差がある。
有意差を判断するための手法
p値と有意水準
統計的検定では、p値(p-value)を用いて有意差を判断します。
- p値:帰無仮説が正しいと仮定した場合に、観測されたデータが得られる確率。
- 有意水準(α):p値と比較する基準値。一般的には5%(0.05)や1%(0.01)が用いられます。
p値が有意水準を下回る場合、帰無仮説を棄却し、対立仮説を採択します。これにより「統計的に有意な差がある」と判断されます。
適切な検定方法の選択
以下のフローチャートに従って、適切な検定方法を選択することができます:
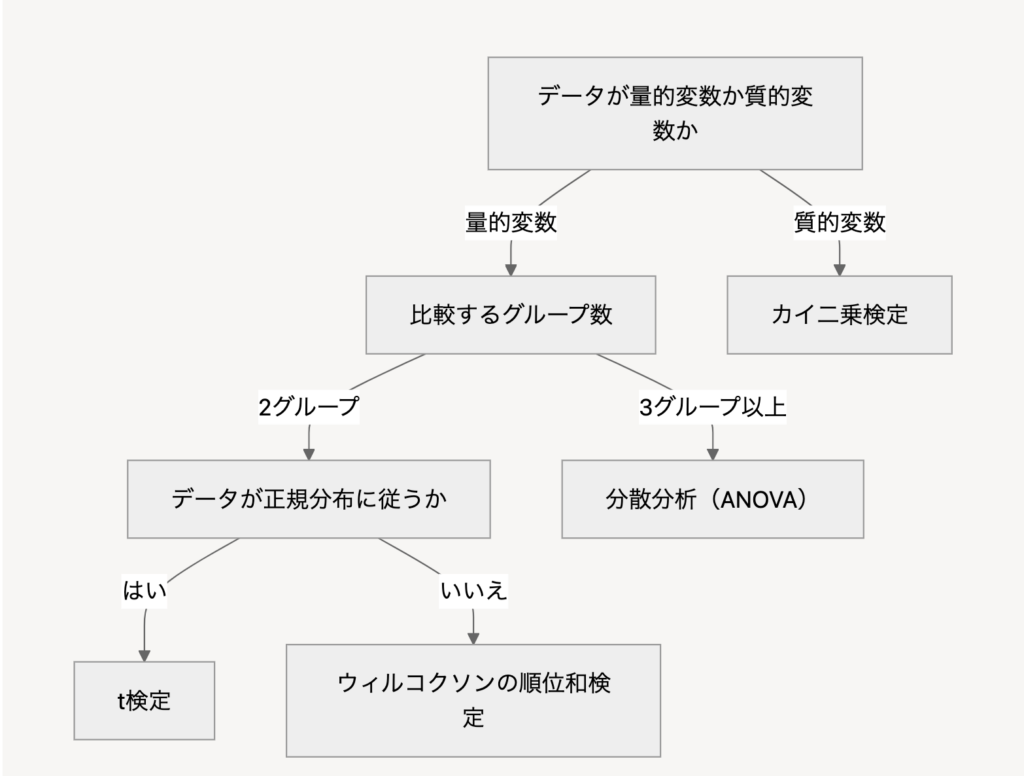
主な検定方法の特徴
- t検定:2つのグループの平均値を比較する際に使用。
- 対応なし:独立した2群の比較
- 対応あり:同一群の前後比較
- カイ二乗検定:カテゴリーデータの分布を比較する際に使用。
- 独立性の検定:2つの変数間の関連を確認
- 適合度の検定:理論値との比較
- ANOVA(分散分析):
- 一元配置:1つの要因による比較
- 二元配置:2つの要因による比較
統計ソフトウェアでの実行方法
Excelでの実行手順
- t検定の場合:
- 「データ」タブ →「データ分析」→「t検定」を選択
- データ範囲を指定し、有意水準を設定
- 出力範囲を選択して実行
2. カイ二乗検定の場合:
- 関数「CHISQ.TEST」を使用
- 観測値範囲と期待値範囲を指定
Pythonでの実行例
from scipy import stats
# t検定の例
t_stat, p_value = stats.ttest_ind(group1, group2)
# カイ二乗検定の例
chi2, p_value = stats.chi2_contingency(contingency_table)有意差の具体例
例1:新薬の効果検証
新薬の効果を検証するために、治療群とプラセボ群の血圧変化を比較したとします。
- 治療群の平均血圧変化:-10 mmHg
- プラセボ群の平均血圧変化:-2 mmHg
- p値:0.03
この場合、p値が有意水準(0.05)を下回るため、「新薬はプラセボよりも効果がある」と結論づけられます。
例2:マーケティング施策の効果測定
新しい広告キャンペーンの効果を検証するために、広告を見たグループと見ていないグループの購入率を比較したとします。
- 広告を見たグループの購入率:15%
- 広告を見ていないグループの購入率:10%
- p値:0.01
この場合もp値が有意水準を下回るため、「広告キャンペーンは購入率を向上させた」と判断できます。
有意差の誤用と注意点
1. p値の過度な重視
よくある誤解:
- p < 0.05なら必ず重要な差がある
- p > 0.05なら差が全くない
正しい解釈:
- p値は「差がない確率」を示すのみ
- 実務的な重要性は効果量で判断する
2. サンプルサイズの影響
- 大きすぎるサンプル:
- わずかな差でも有意になりやすい
- 実務的な重要性の判断が必要
- 小さすぎるサンプル:
- 検出力が低下
- 第二種の過誤のリスク増加
3. 多重比較の問題
- 問題点:
- 検定回数が増えると偽陽性のリスクが上昇
- 5%の有意水準で20回検定すると、1回は偶然で有意になる可能性
- 対策:
- ボンフェローニ補正の適用
- FDR(False Discovery Rate)制御
業界別の活用事例
1. 製造業での品質管理
- 工程改善の効果検証:
- 改善前後の不良率比較
- 管理図による工程能力の評価
- 材料変更の影響分析:
- 強度試験データの比較
- 耐久性テストの結果分析
2. 医療分野での臨床試験
- 新薬の有効性評価:
- プラセボ対照試験
- 非劣性試験での既存薬との比較
- 治療法の比較:
- 生存率の差の検定
- QOL指標の変化分析
3. マーケティングでの意思決定
- A/Bテスト:
- ランディングページの最適化
- メールマーケティングの文言比較
- 顧客セグメント分析:
- 購買行動の違いの検証
- 顧客満足度の比較
よくある質問(FAQ)
Q1: サンプルサイズはどのくらい必要?
A1: 検出したい効果量、検定力、有意水準から計算可能。一般的な目安として、各群30以上が望ましい。
Q2: 両側検定と片側検定はどちらを選ぶ?
A2: 特別な理由がない限り、両側検定を選択。片側検定は方向性が明確な場合のみ。
Q3: 効果量とは何か?
A3: 差の大きさを標準化した指標。Cohen’s dやr²などがある。実務的な重要性の判断に使用。
まとめ
有意差は、統計学的検定を通じてデータの差が偶然ではないことを示す重要な概念です。p値や有意水準を活用し、帰無仮説と対立仮説を検証することで、データに基づいた客観的な意思決定が可能になります。ただし、p値だけに依存せず、効果量や信頼区間、サンプルサイズなども考慮することが重要です。
ビジネスや研究において、有意差を正しく理解し活用することで、より信頼性の高い結論を導き出し、意思決定の質を向上させることができます。特に、適切な検定方法の選択、ソフトウェアでの実行、結果の解釈において、本記事で解説した点に注意を払うことで、より確かな分析が可能となるでしょう。

